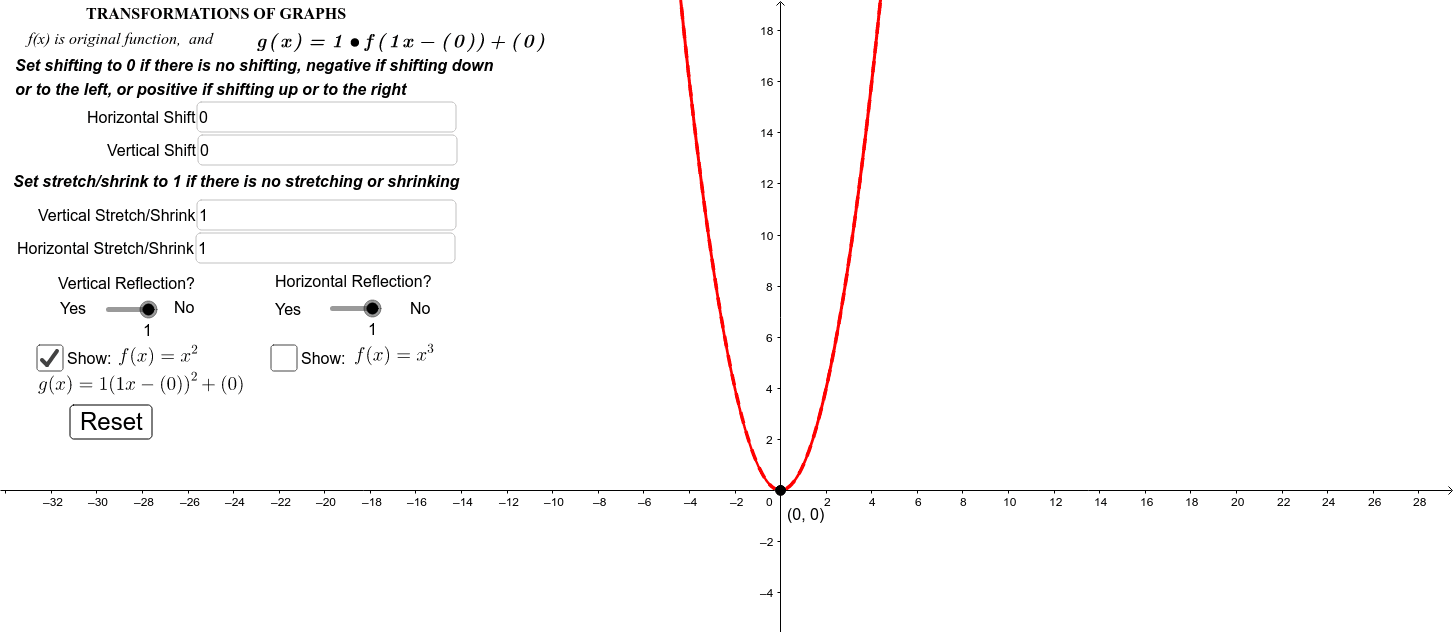
Transformations can be combined within the same function so that one graph can be shifted, stretched, and reflected If a function contains more than one transformation it may be graphed using the following procedure Steps for Multiple Transformations Use the following order to graph a function involving more than one transformation 136 Graphing Transformations You have learned how to move a parabola around a set of axes, write equations, sketch graphs, and model situations The graph of y = x2 is called the parent graph for the family of parabolas because every other parabola can be seen as a transformation of that one graphGraphs and Transformations wwwnaikermathscom 2 Figure 1 Figure 1 shows a sketch of the curve with equation y = x 2, x ≠ 0 The curve C has equation y = x 2 − 5, x ≠ 0, and the line l has equation y = 4x 2 (a) Sketch and clearly label the graphs of C and l on a single diagramOn your diagram, show clearly the coordinates of the points where C and l cross the
How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic
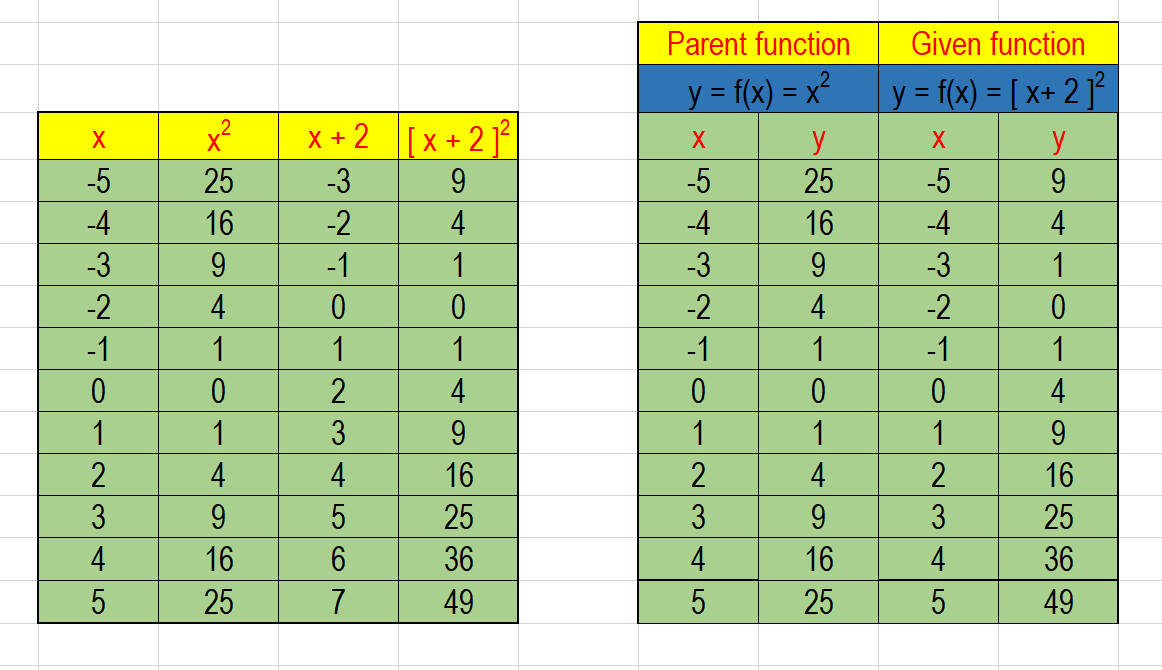
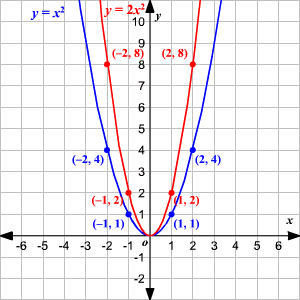
Graph of y=x^2 transformations
Graph of y=x^2 transformations-Solutions Problem 1 Submit an equation that will move the graph of the function y = x 2 left 7 units and down 3 units Solution From the parent function y = x 2, if it is moved 7 units to the left, we will have the function y = (x 7) 2 Further, if it is moved 3 units down, the function will beC < 0 moves it down We can move it left or right by adding a constant to the xvalue g(x) = (xC) 2




How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic
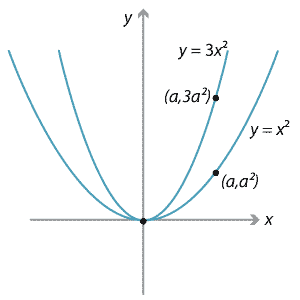
Transformations and Functions Quiz Review Name Ibrahim Ismail _____ Algebra 2A () For each graph, fill in the information 1 Parent Function Name Quadratic _____ Equation of Parent Function y=x^2 _____ Transformations Reflected across the xaxis, up 5, left 4Algebra Describe the Transformation y=x^2 , y=3x^2 y = x2 y = x 2 , y = 3x2 y = 3 x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = 3x2 y = 3 x 2 is g(x) = 3x2 g ( x) = 3 x 2 f (x) = x2 f ( x) = x 2 g(x) = 3x2 g ( x) = 3 x 2Graph Transformations There are many times when you'll know very well what the graph of a particular function looks like, and you'll want to know what the graph of a very similar function looks like In this chapter, we'll discuss some ways to draw graphs in these circumstances
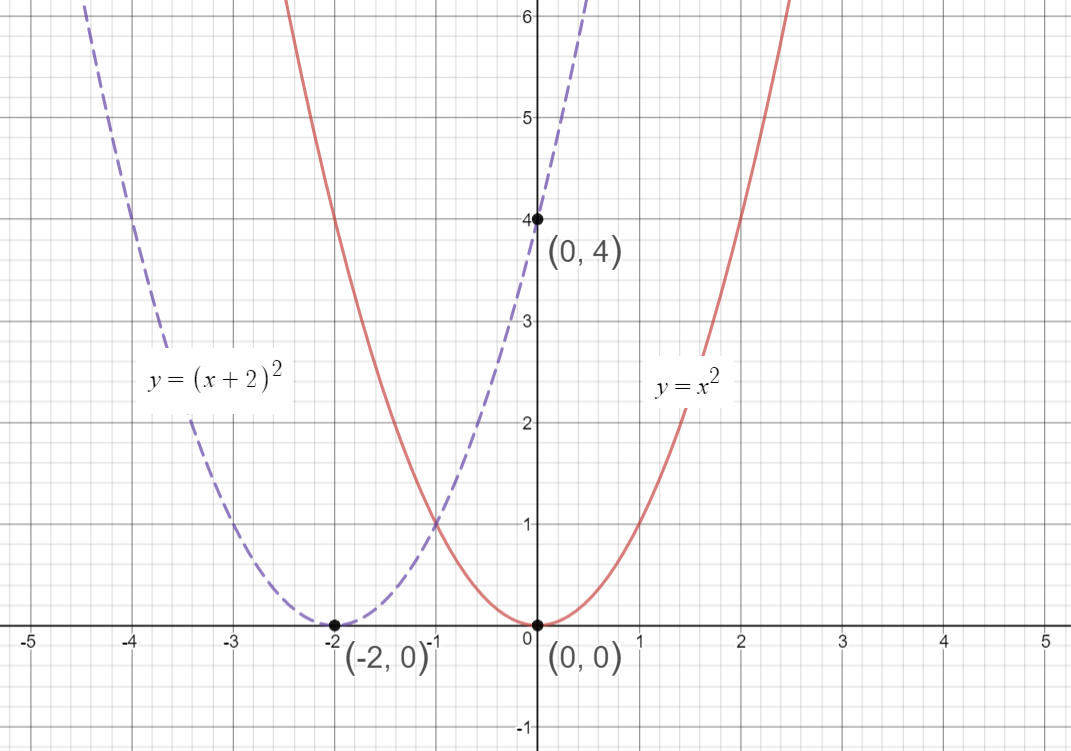
Describe the transformations to the graph of y=x^2 that result in the graph of y=(x2)^23 sabbychun is waiting for your help Add your answer and earn points About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators15) The graph of y= x2 is on the left;
Answer choices a reflection across the line x = 4 a reflection across the line y = 4 a translation shifting f (x) 4 units to the leftGraph transformations Given the graph of a common function, (such as a simple polynomial, quadratic or trig function) you should be able to draw the graph of its related functionStep 1 By graphing the curve y = x 2, we get a open upward parabola with vertex (0, 0) Step 2 Here 1 is subtracted from x, so we have to shift the graph of y = x 2, 1 unit to the right side Step 3



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic




Exploring Transformations And Parent Graphs
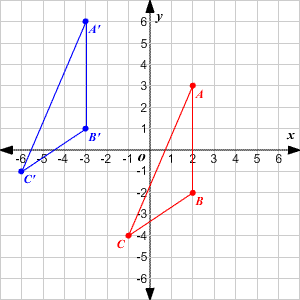
To start, let's consider the quadratic function y=x 2 Its basic shape is the redcoloured graph as shown Furthermore, notice that there are three similar graphs (bluecoloured) that are transformations of the original g(x)=(x5) 2 Horizontal translation by 5 units to the right; Explanation If you know the graph of a function y = f (x), then you can have four kind of transformations the most general expression is h and v are, respectively, horizontal and vertical translations In your case, starting from f (x) = x2, you have A = 1 and w = 1 Being multiplicative factors, they have non effectBecause \(f\) graphs to a line segment, \(g\) will also graph to a line segment (None of the transformations introduce a bend that was not already there) As such, we can just track the endpoints through the transformations, plot the new endpoints, and connect those with a



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic



Transformations Of Functions
Graph the function f (x) = 2x^2 4x 1 by starting with the graph of y = x^2 and using transformations (shifting, stretching/compressing and/or reflecting) Use the graphing tool to graph the function We can compare the graph of this function to the graph of the parent y = x 2 the graph represents a vertical stretch by a factor of 2, a horizontal shift 3 units to the right, and a vertical shift of 1 unit We can use this relationship to graph the function y = 2(x 3) 2 1 You can start by sketching y = x 2 or y = 2x 2 Then you can shift the graph 3 units to the right, and up 1SURVEY 1 seconds Q Which transformation maps the graph of f (x) = x 2 to the graph of g (x) = (x 4)2?



Read Transform Linear Functions Intermediate Algebra
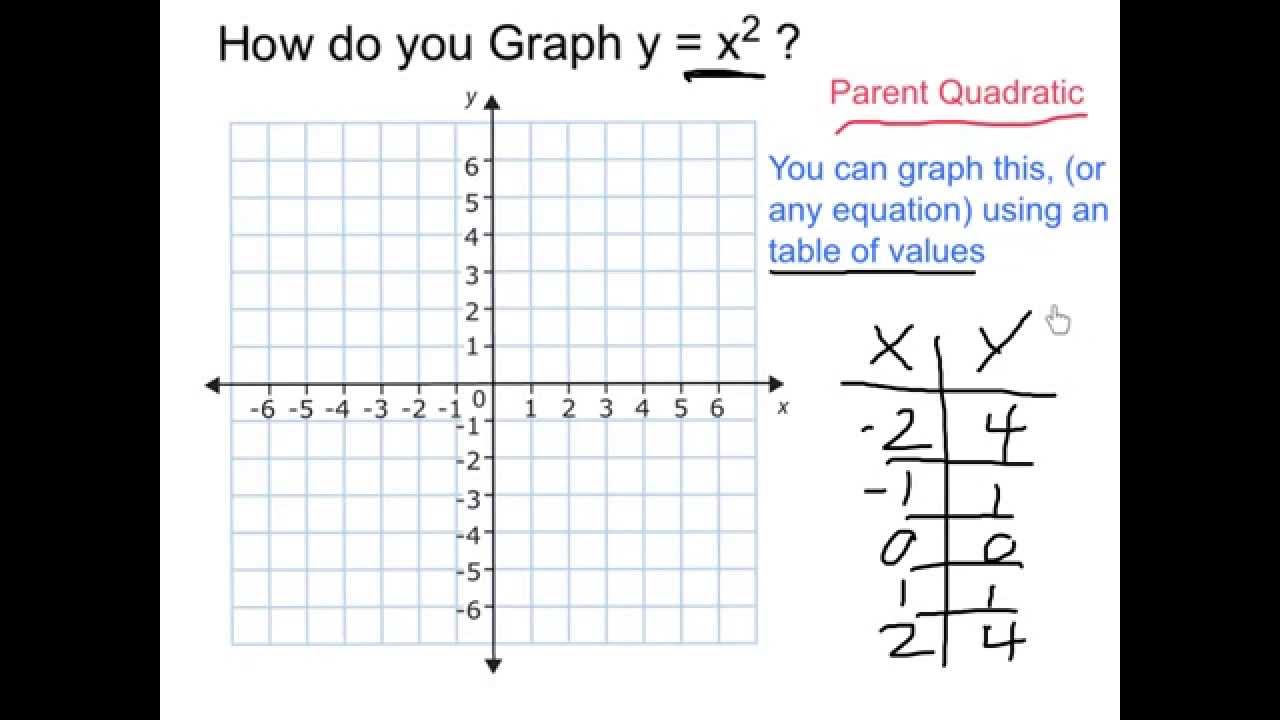



Graph Y X 2 Youtube
Graph Of Y X 2 Transformations ihličnaté stromy v kvetináči hviezda v súhvezdí orol inovovaný štátny vzdelávací program isced 1 hugolín gavlovič valaská škola if f x x 4 2x 3 3x 2 ax b informovaný súhlas rodiča výlet vzor ii rákóczi ferenc gimnázium budapest incheba vianocne trhy 19 impresia východ slnka hviezdoslavov180 seconds Q Which transformation maps the graph of f (x) = x 2 to the graph of g (x) = (x 4)2?The transformations of the graph of y = x^2 that will produce the graph of y = (x2)^2 3 A) shifts left 2 units, up 3 units, and reflect across the xaxis B) shifts right 2 units, down 3 units,




Transformations Of Quadratic Functions College Algebra



Jdlogo Home Functions Defined Functions You Should Know Transformations Of Quadratics Translations Reflections Inverses Stretches Combinations Combining Functions Review Test Unit 2 Functions And Transformations Lesson 3a
Y x 2 5 y x 2 y x 3 5 2 Examples 1 Using the given key points from the graph U= √ T, map the new points for each given transformation Transformation of = √Describe a sequence of two geometrical transformations that maps the graph of y = x^2 onto the graph of y = 4x^2 5 I thought it'd be a Scale Factor of 1/2 and a translation of (5, 0) But the answer is a Scale Factor of 1/4 and a translation of (0, 5) 17 Transformations In this section, we study how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas The transformations we will study fall into three broad categories shifts, reflections and scalings, and we will present them in that order




Transformations Of The 1 X Function Video Lesson Transcript Study Com
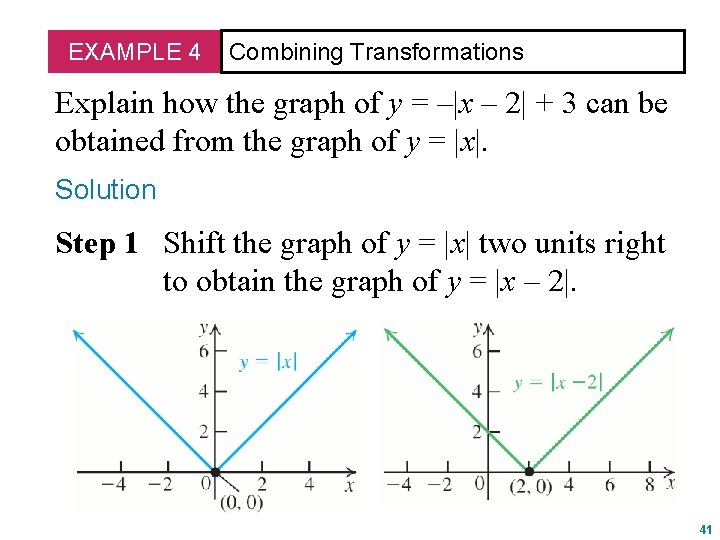



Transformations Of Section Functions 2 7 2 Learn
A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x 2 3 looks like thisHere are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;Answer choices a reflection across the line x = 4 a reflection across the line y = 4 a translation shifting f (x) 4 units to the left a translation shifting f (x) 4 units to the right
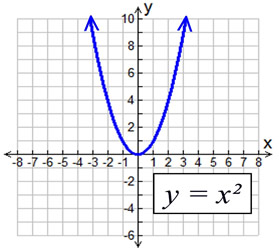



Parabola Parent Function Mathbitsnotebook Ccss Math
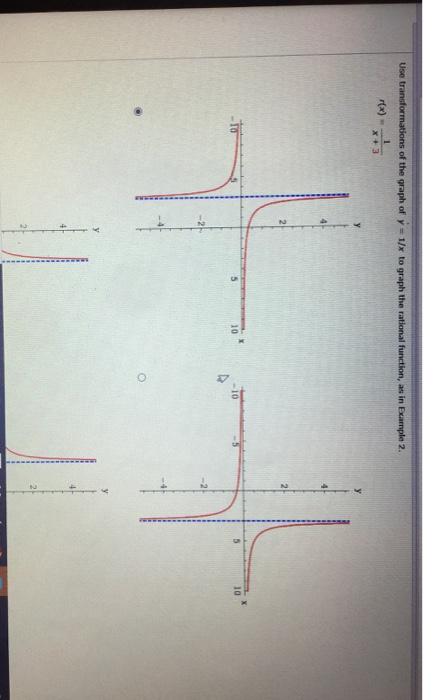



Use Transformations Of The Graph Of Y 1 X To Graph Chegg Com
To obtain the graph of f ()x =ax2 from the graph ofy =x2, multiply each y‐coordinate on the graph of y =x2 by a Example 3 Use the graph of y =x2 to graph the quadratic function Based on the graph,Y = x2 y = x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 y = x 2 is g(x) = x2 g ( x) = x 2 f (x) = x2 f ( x) = x 2 g(x) = x2 g ( x) = x 2 The transformation being described is from f (x) = x2 f ( x) = x 2 to g(x) = x2 g ( x) = x 2Using our knowledge of reflections across the yaxis, the graph of y 2 (x) should look like the base graph g(x) reflected across the yaxis To check this, we can write y 2 ( x ) as, y 2 ( x ) = g ( x ) = ( x ) 3 ( x ) 2 4( x ) 4 = x 3 x 2 4 x 4,



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic



Solution I Have A Question That States A Use The Transformations On The Graph Of Y X 2 To Determine The Graph Of Y X 5 2 9 B Using The Graph Of F X X 2 As A Guide Graph
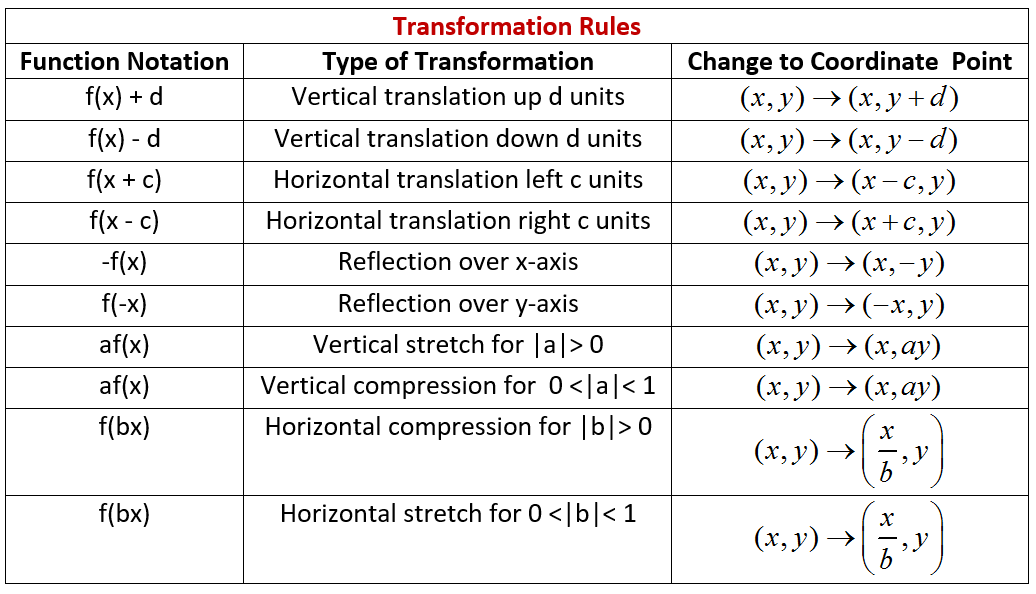
1 To obtain the graph of y = (x 8)2, shift the graph of y = x2 2 To obtain the graph of y = x2 6, shift the graph of y = x2 A ball is thrown straight up from a height of 3 ft with a speed of 32 ft/s Its height above the ground after x seconds is given by the quadratic function y = 16x2 32x 317 Transformations 123 2 to all of the xvalues of the points on the graph of y= f(x) to e ect a shift to the right 2 units Generalizing these notions produces the following resultH(x)=x 2 5 Vertical translation by 5 units upwards;
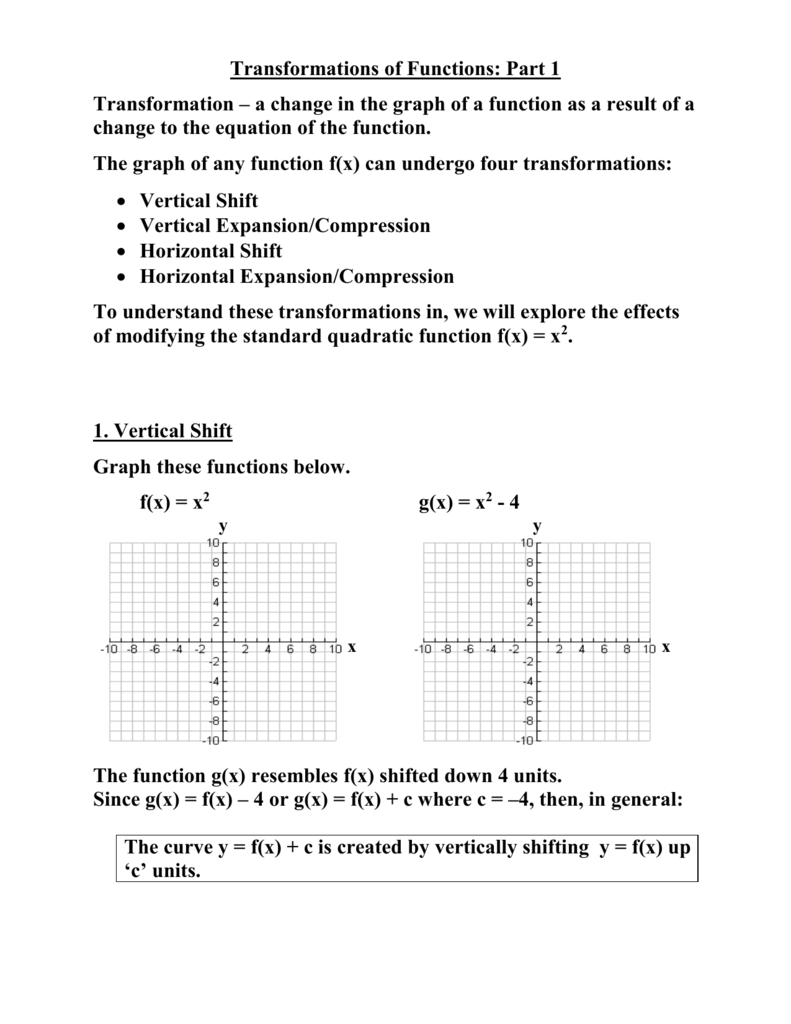



Transformations Of Functions Part 1
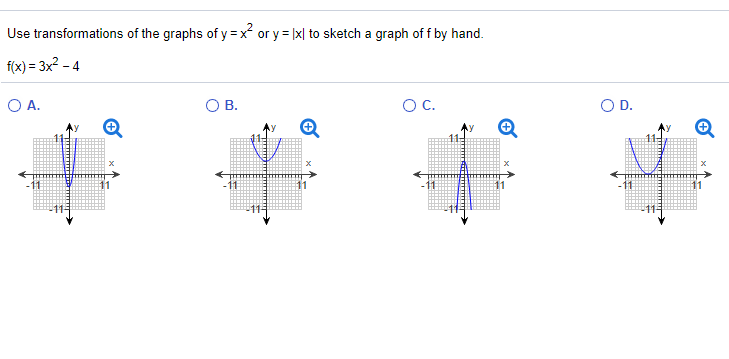



Solved Use Transformations Of The Graphs Of Y X2 Or Y Xl Chegg Com
3) Describe, using transformations how the graph of y=x^2 can be transformed into the graph of the quadratic relation (16 marks) a) y= 5x^24 c) y = 1/4 (x5)^2 b) y=3(x2)^27 d) T (x,y) → (x2,5y3) 4) List the features of this parabola and the step patternGraph Transformations In order to have graph transformations, we need to know first the different rules of transformations such as translation, reflection, compression, and stretchNavigate all of my videos at https//sitesgooglecom/site/tlmaths314/Like my Facebook Page https//wwwfacebookcom/TLMaths/ to keep updat




Describe The Transformations Of The Graph Of Y X That Will Produce The Graph Of Y X 2 2 3 Brainly Com
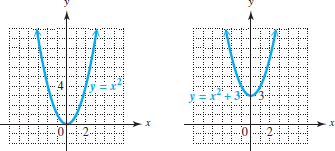



Solved If You Compare The Graph Of Y X2 3 To The Graph Of Y Chegg Com
Problem 81 Easy Difficulty (A) Starting with the graph of y = x 2, apply the following transformations (i) Shift downward 5 units, then reflect in the x axis (ii) Reflect in the x axis, then shift downward 5 units A horizontal translation 60 is a rigid transformation that shifts a graph left or right relative to the original graph This occurs when we add or subtract constants from the \(x\)coordinate before the function is applied For example, consider the functions defined by \(g(x)=(x3)^{2}\) and \(h(x)=(x−3)^{2}\) and create the following tables galactiicdoom2 Answer Sketch the graph of y=7^x Reflect the graph across the yaxis to show the function y=7^x Stretch the graph vertically by a factor of 3 to show the function y=3*7^x Shift the graph up 2 units to show the function y=3*7^x2 Stepbystep explanation



Content Transformations Of The Parabola




Using Transformations To Graph Functions
23 Transformations of Graphs 79 happens for each kind of transformation we examine Accordingly, we will show lots of graphs, but for your benefit, we strongly encourage you to use your graphing calculator to draw each graph yourself The first example asks for graphs of vertical shifts of two core graphs While The graph of y = −(x 2)2 − 2 is graph { (x2)^22 10, 10, 5, 5} Its transformation is a reflection over the xaxis, a translationHow to apply this to a graph Example You are given the function y = x 2 4 Sketch the graph of y = 2(x 2 – 4) In the transformation y = af(x), a = 2 so every value of y will double and the values of x will stay the same Sometimes when you translate a function, you will be expected to label the significant points that have been translated




Parabola Transformations Match Up 1 Distance Learning Algebra Quadratics High School Mathematics




Symmetry Transformations And Compositions
The graphs of many functions are transformations of the graphs of very basic functions The graph of y = x2 is the reflection of the graph of y = x2 in the xaxis Example The graph of y = x2 3 is the graph of y = x2 shifted upward three units This is a vertical shift x y4 4 448 8 y = x2 y = x2 3 y = x2Sketch the graph of Solution Begin with the basic function defined by and shift the graph up 4 units Answer A horizontal translation A rigid transformation that shifts a graph left or right is a rigid transformation that shifts a graph left or right relative to the original graphA graph can be translated horizontally, vertically or in both directions Translations parallel to the yaxis \ (y = x^2 a\) represents a translation parallel to the \ (y\)axis of the graph of \




Graphing Square And Cube Root Functions Video Khan Academy
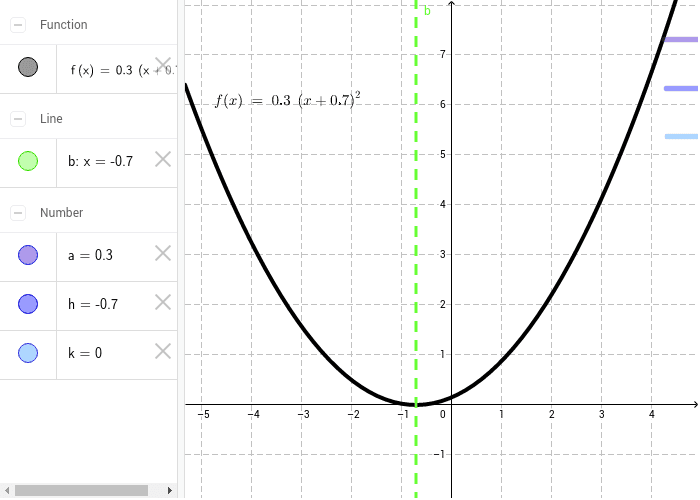



Transformations To The Graph Of Y X 2 Geogebra
The graph of y= 3(x 5)2 7 is on the right If one looks carefully, one can see that the labels on the yaxis have changed, otherwise the graphs are the same Figure 13 Graphs of y= x2 and y= 3(x 5)2 7 (Generated by the author using Sage) There are four types of transformations we will study in this



Transformations Of Functions Mathbitsnotebook A1 Ccss Math




Content Transformations Of The Parabola



Transformations Mrs F X
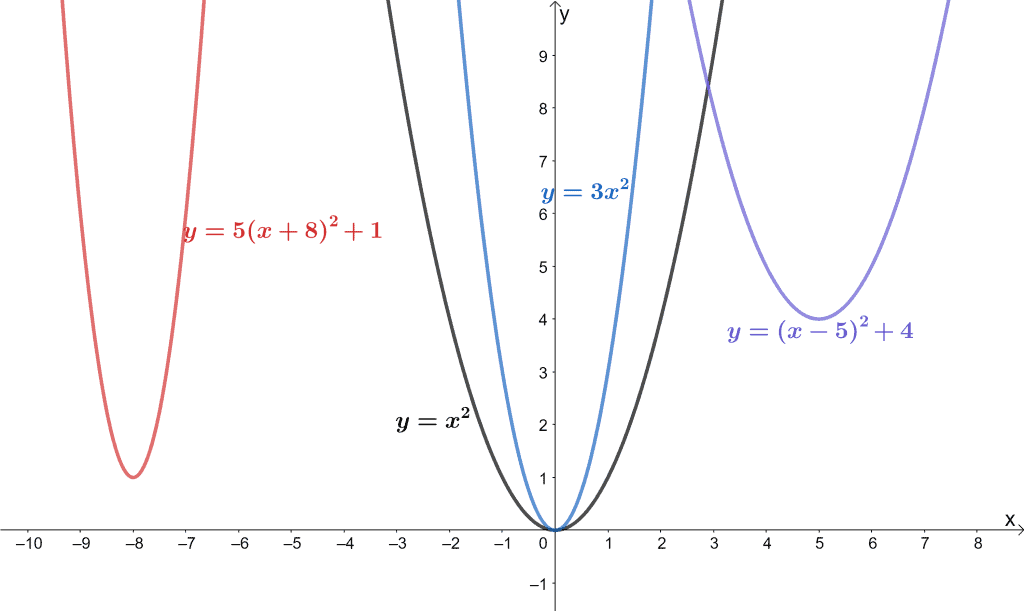



Transformations Of Functions Explanation Examples



Quadratic Transformations Part 1 Activity Builder By Desmos
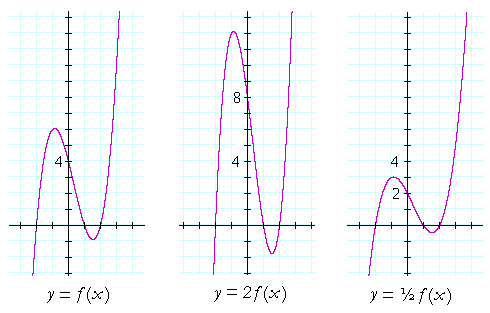



Translations Of A Graph Topics In Precalculus



Transformations Of The Graph Y Sqrt X Geogebra
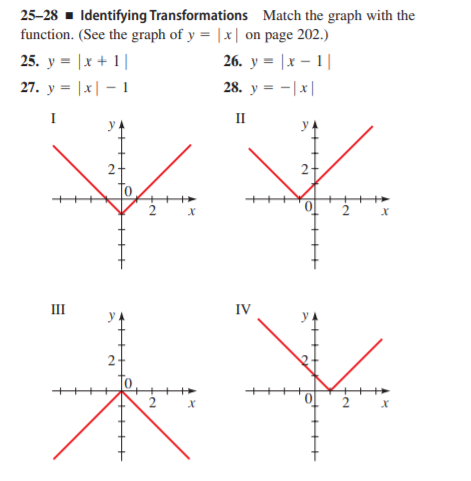



Answered 25 28 Identifying Transformations Bartleby
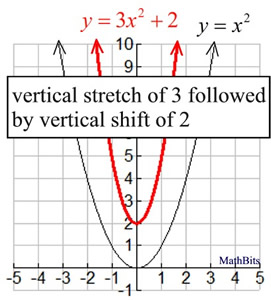



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math



Transformations Of Functions Mathbitsnotebook A1 Ccss Math



Www Tamdistrict Org Cms Lib Ca Centricity Domain 348 1 sept 17 adv alg wkst and key Pdf




The Transformation Of The Graph Of A Quadratic Equation Matherudition




Combining Transformations Ck 12 Foundation
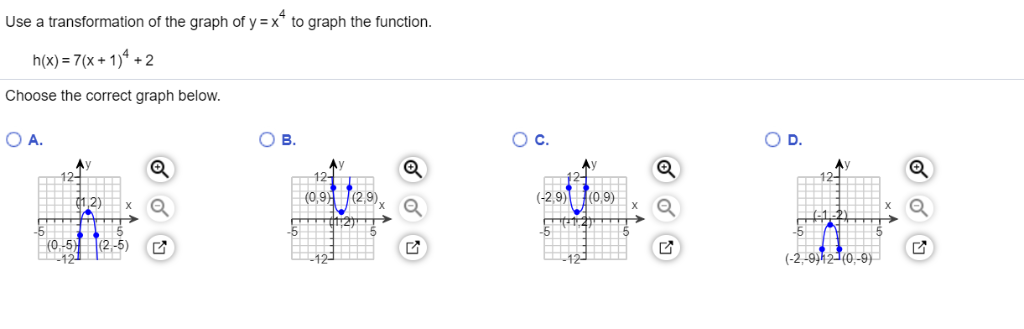



Use A Transformation Of The Graph Of Y X 4 To Graph Chegg Com
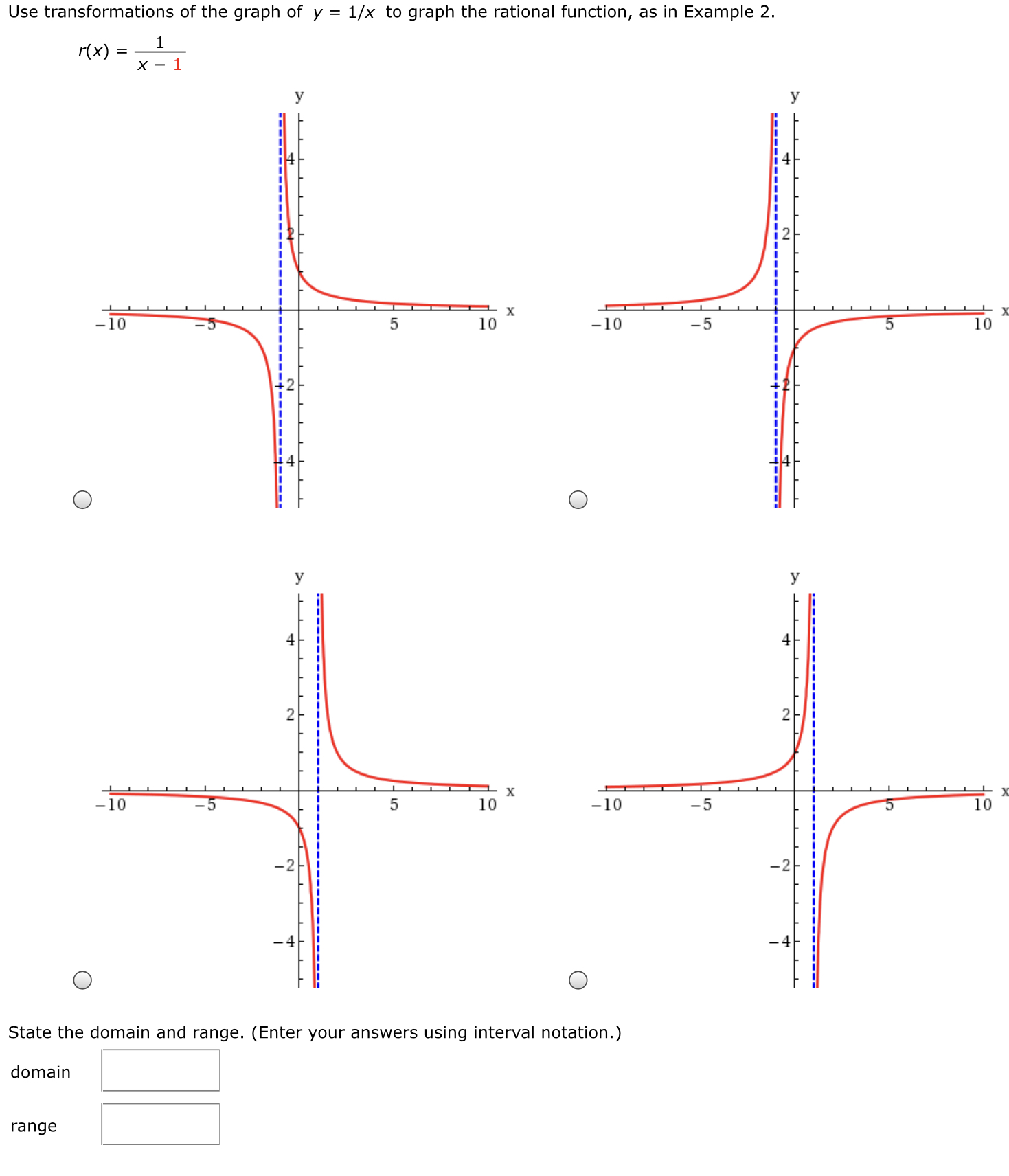



Answered Use Transformations Of The Graph Of Y Bartleby




Transformations Of Functions Ck 12 Foundation




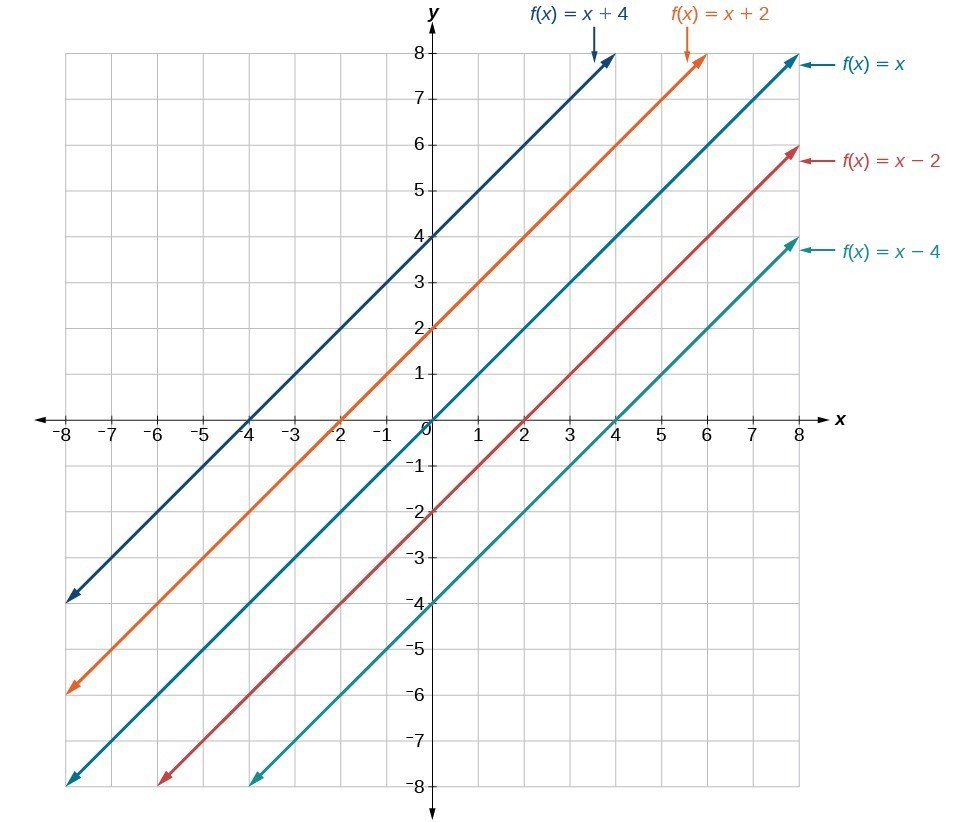
Transformations Of Y X Ck 12 Foundation




How To Graph Transformations Of Functions 14 Steps
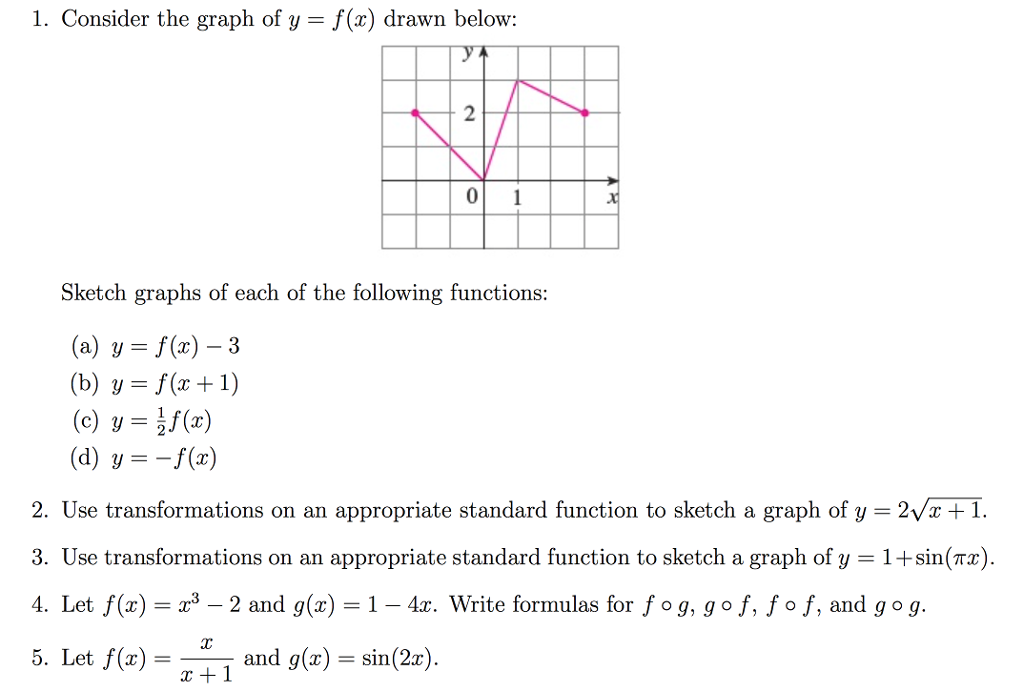



1 Consider The Graph Of Y F X Drawn Below 2 0 Chegg Com




Transforming Exponential Graphs Example 2 Video Khan Academy
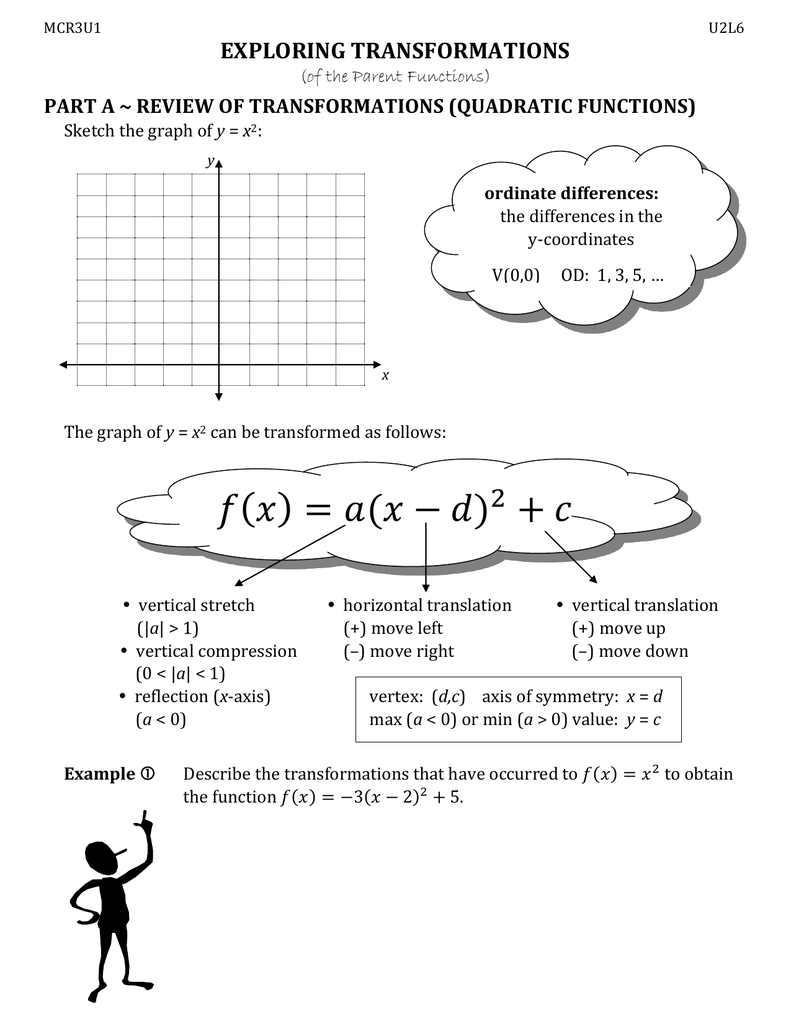



Exploring Transformations Of Parent Functions
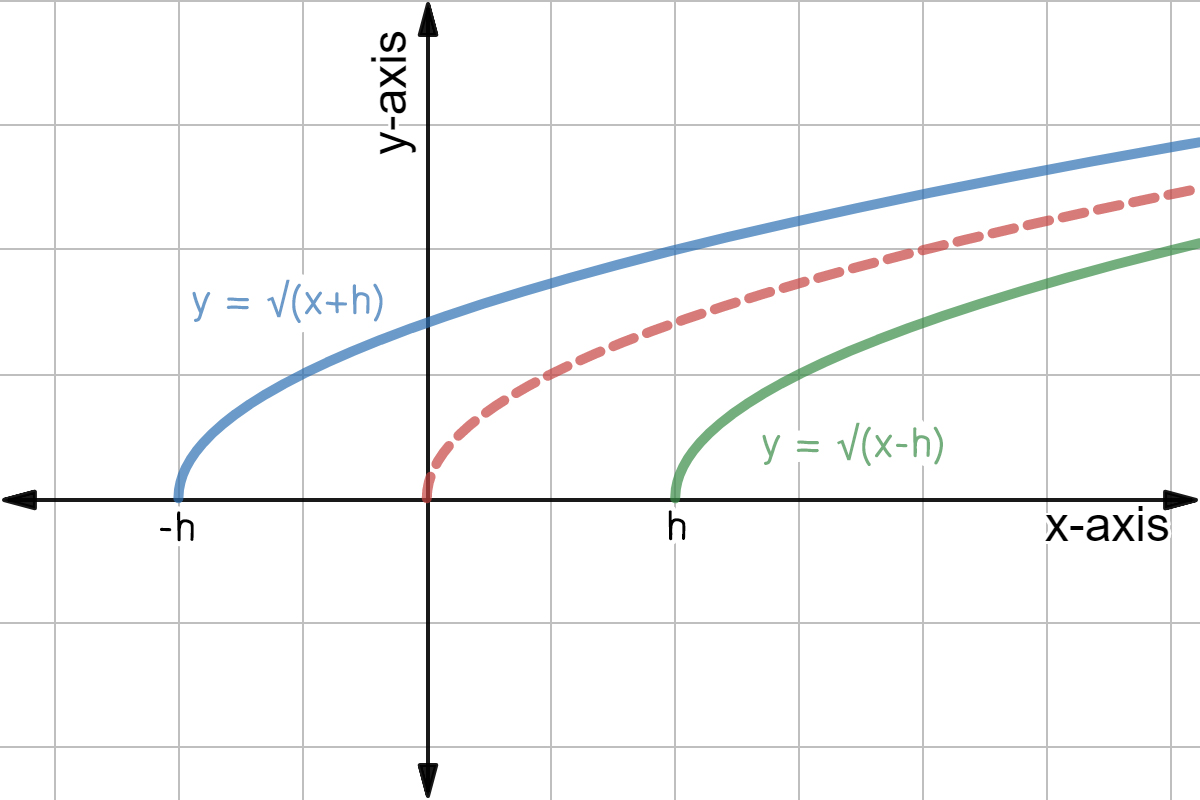



Horizontal Translation Of Square Root Graphs Expii
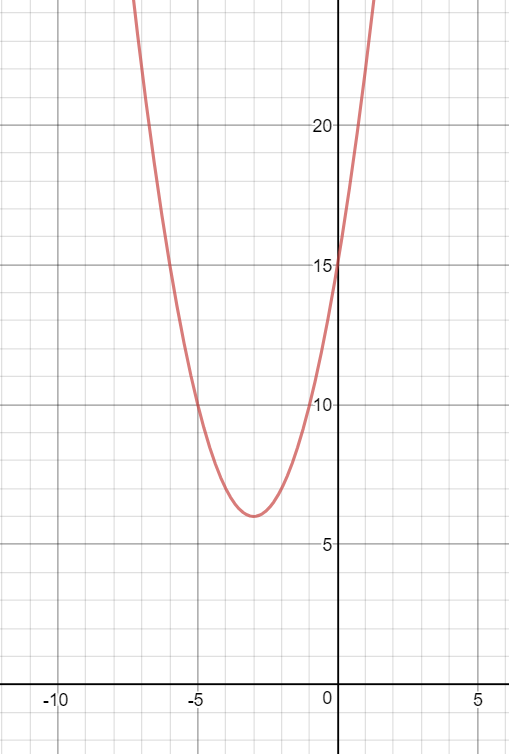



How Do You Sketch The Graph Of Y X 3 2 6 And Describe The Transformation Socratic
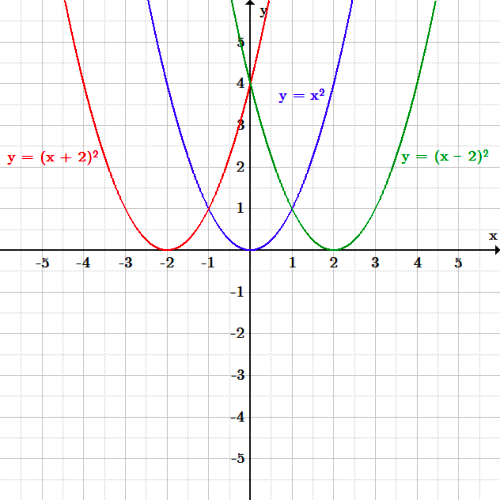



Transformations Boundless Algebra
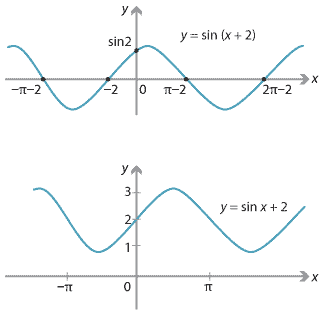



Content Geometric Transformations Of Graphs Of Functions




How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic



1




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation




Transforming Exponential Graphs Example 2 Video Khan Academy
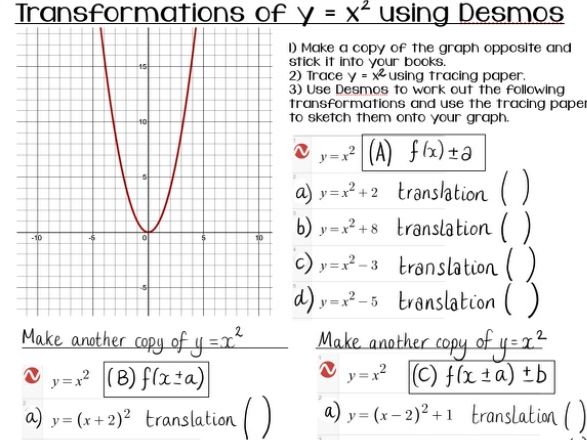



Transformations Of Y X 2 Using Desmos Teaching Resources



Transformation Of Y X 2 And Y X 3 Geogebra




Use Transformations Of The Graph Of Y X4 Or Y X5 Chegg Com



3 5 Transformations Of Functions 2 5 Ncb 502 Corequisite For Mat 1023 Openstax Cnx



Transformations Of Graphs




The Transformation Of The Graph Of A Quadratic Equation Matherudition
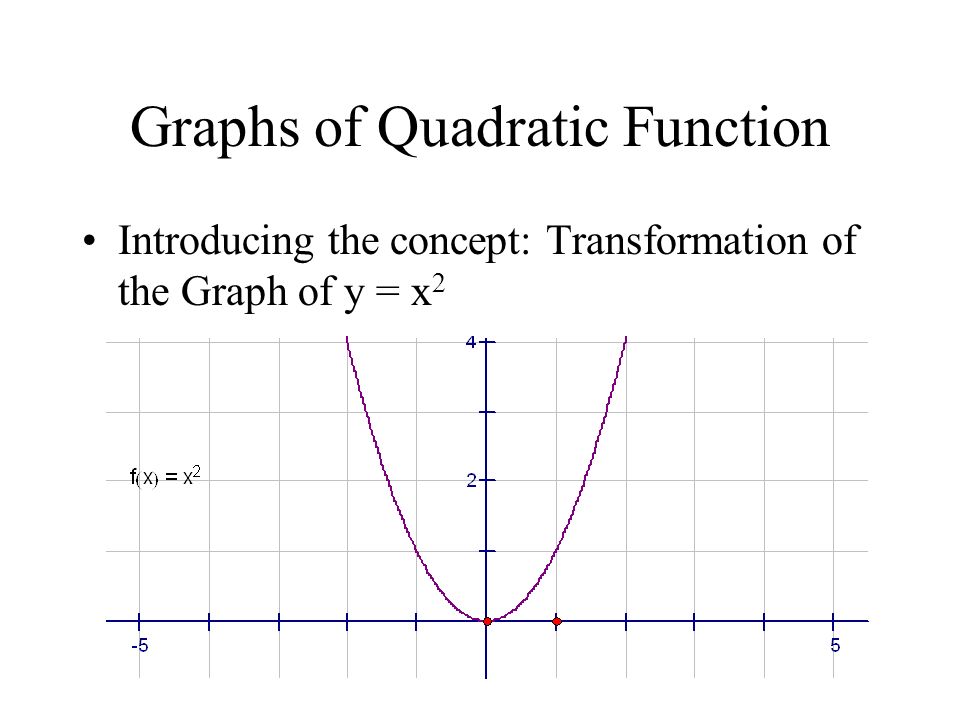



Graphs Of Quadratic Function Introducing The Concept Transformation Of The Graph Of Y X Ppt Download




Transforming Graphs Of Functions Brilliant Math Science Wiki



How Do You Sketch The Graph Of Y X 2 2 2 And Describe The Transformation Socratic




Graph Y X 2 3 Youtube



Graphing Quadratic Equations Using Transformations




Content Transformations Of The Parabola




Sketch The Graph Of The Equation Y X 2 2 3 Study Com




Transformations Ppt Download




The Graph Of The Function Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com
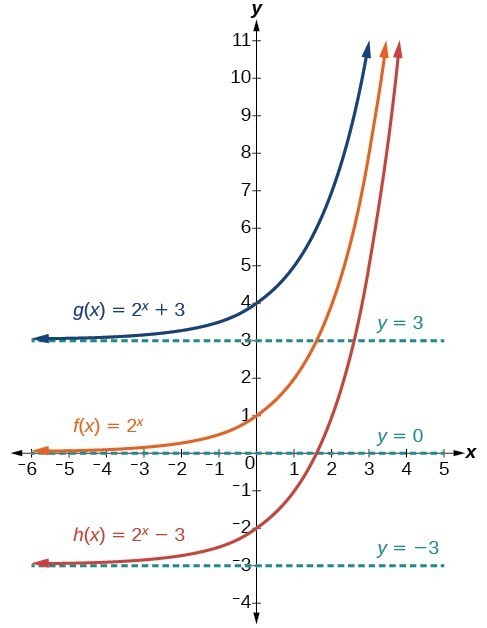



Graph Exponential Functions Using Transformations College Algebra
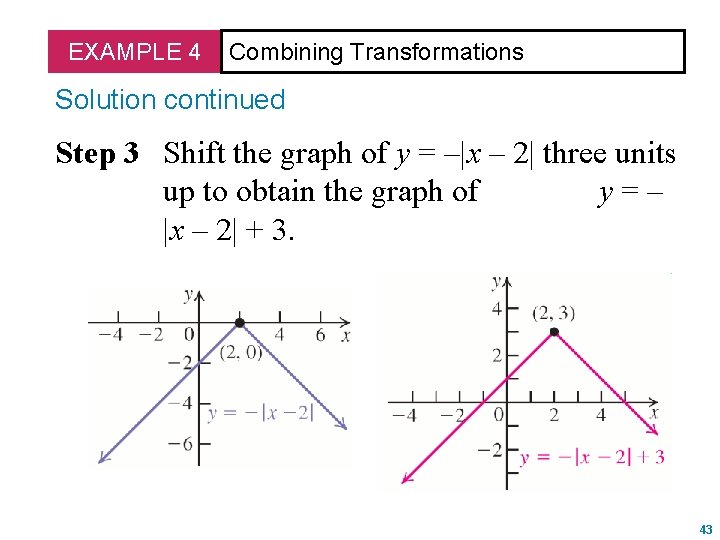



Transformations Of Section Functions 2 7 2 Learn
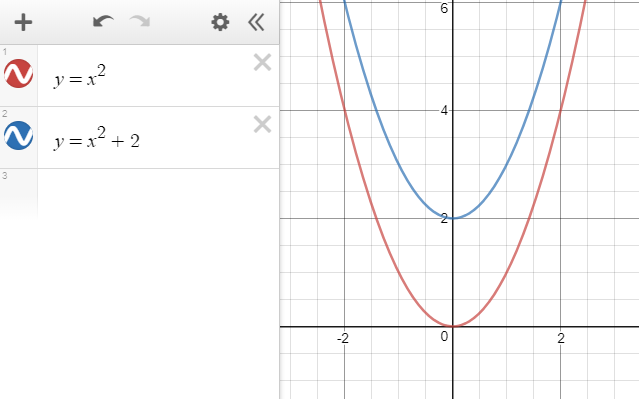



Desmos 2 Transformations Of Graphs Cambridge Maths Hub



Biomath Transformation Of Graphs




Graph Of Y 1 X And With Transformations Youtube
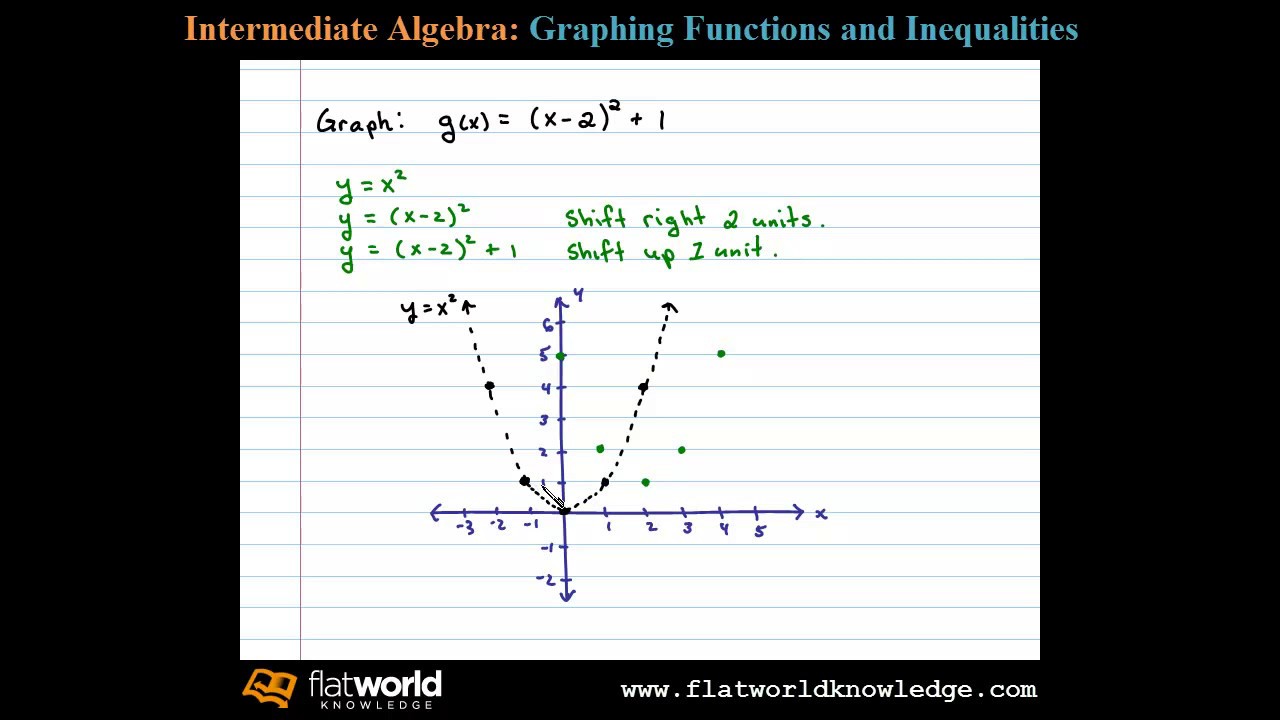



Graph Using Translations G X X 2 2 1 Transformations Algebra Fwk Ia 02 0501 Youtube
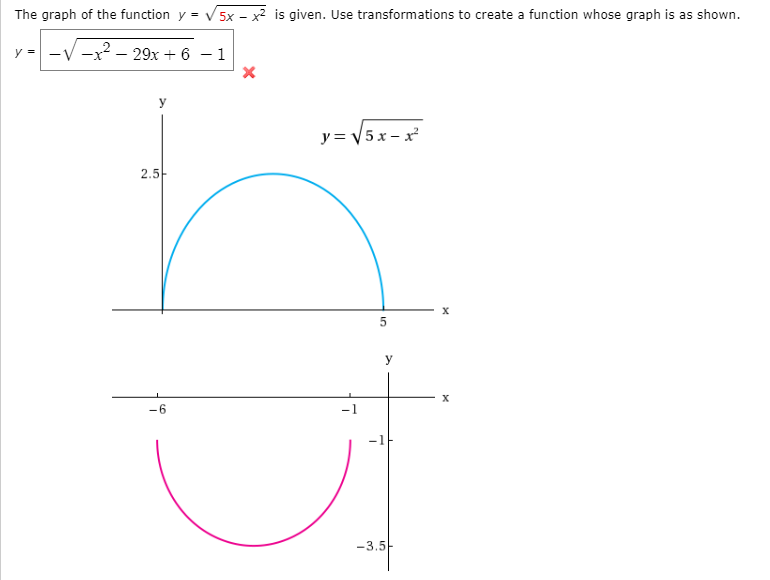



Answered The Graph Of The Function Y V 5x X Bartleby




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
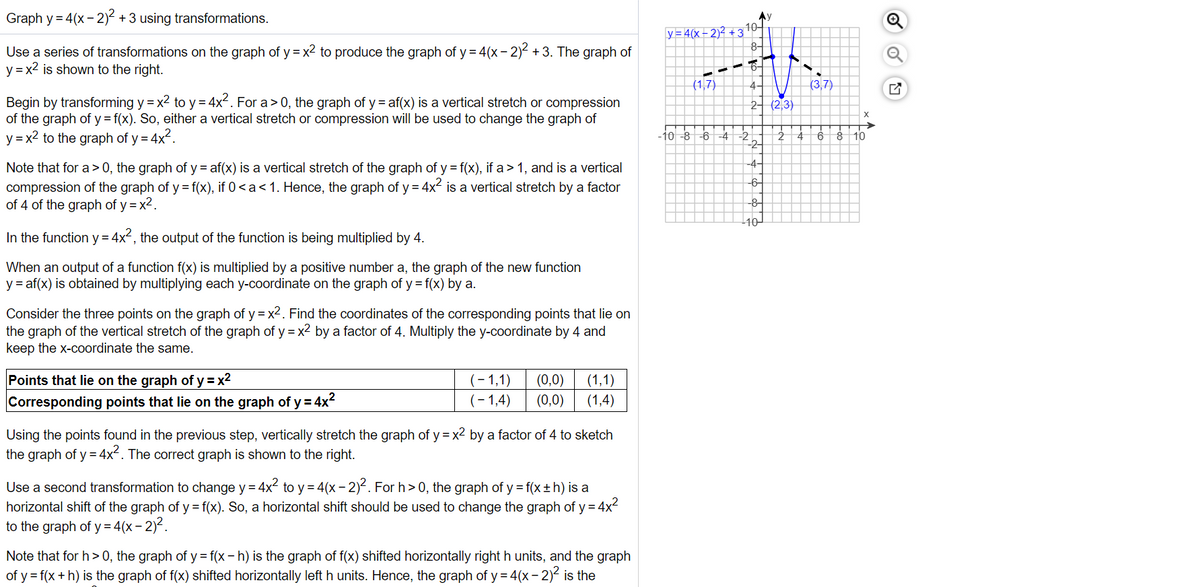



Answered Graph Y 4 X 2 3 Using Bartleby



Solution Describe The Transformation From The Parent Function Y X 6 Y 2 X 5 6 3




Transformations Boundless Algebra
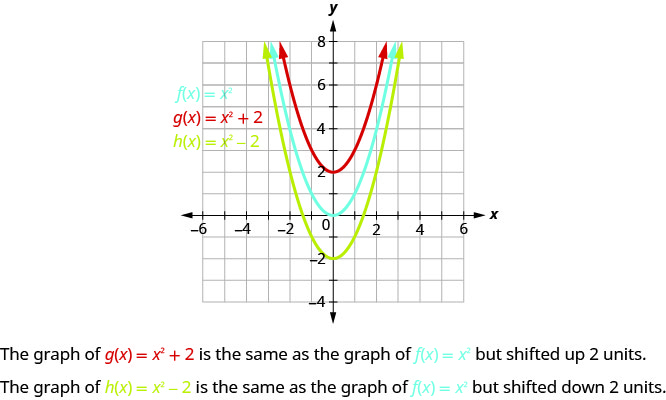



9 8 Graph Quadratic Functions Using Transformations Mathematics Libretexts



1
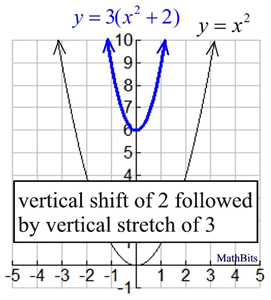



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math




Transformations Of Graphs Stretches Examsolutions Youtube



Biomath Transformation Of Graphs



Using Transformations To Graph Functions




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




The Graph Of Y Sqrt 8x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com
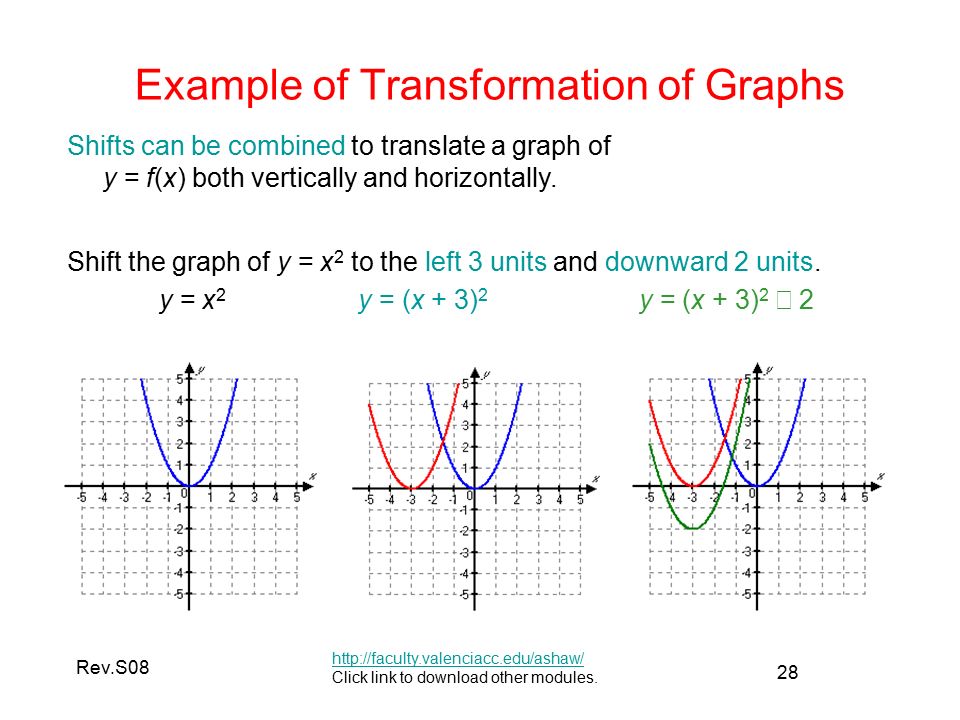



Transformation Of Graphs Ppt Video Online Download




Describe How The Graph Of Y X 2 Can Be Transformed Chegg Com
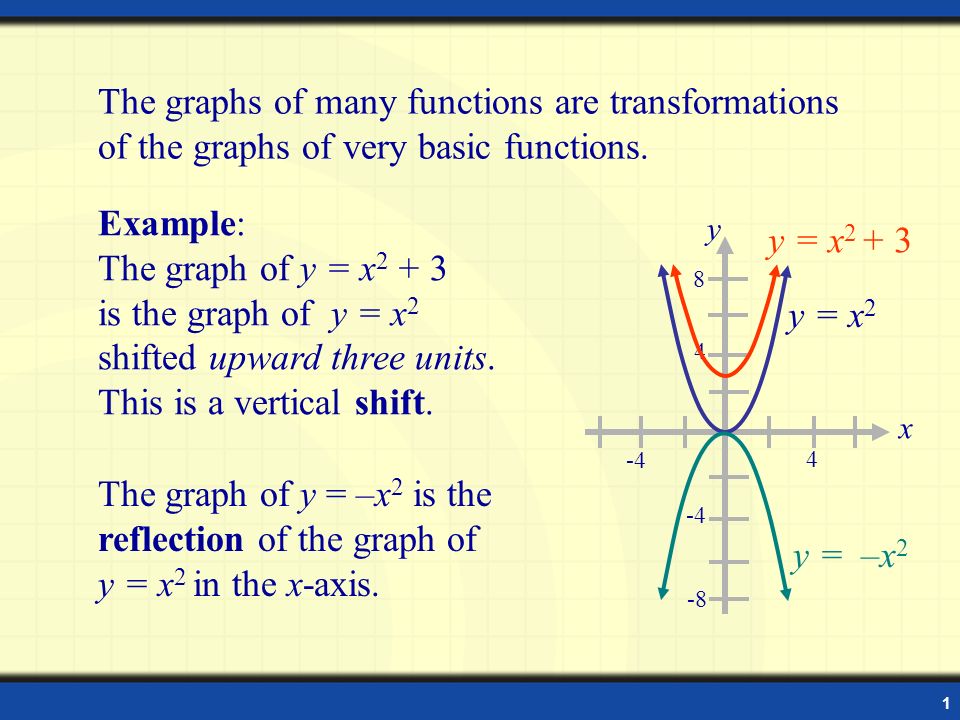



1 The Graphs Of Many Functions Are Transformations Of The Graphs Of Very Basic Functions The Graph Of Y X 2 Is The Reflection Of The Graph Of Y X Ppt Download
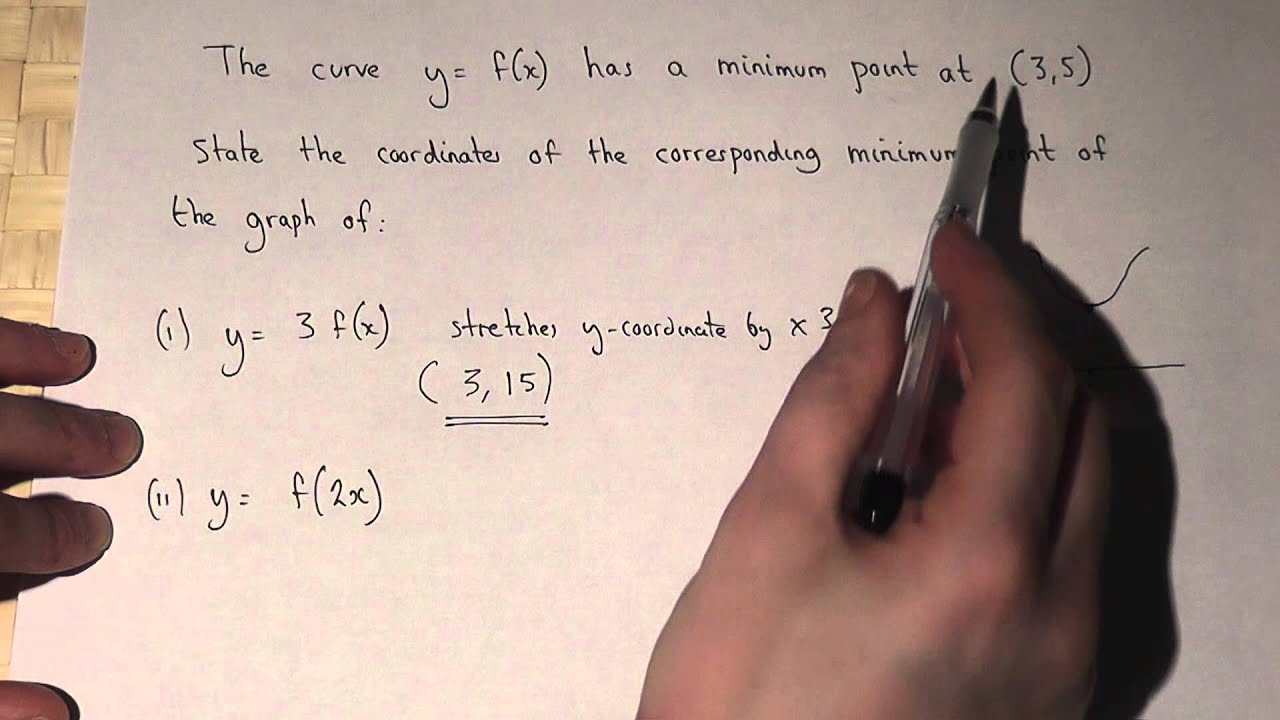



Graph Transformations Y 3f X And Y F 2x Youtube




Content Transformations Of The Parabola



1




Reflecting Functions Examples Video Khan Academy




The Graph Of Y Squareroot 6x X 2 Is Given Use Chegg Com




Graphing Shifted Functions Video Khan Academy




Interpret The Graph Of Frac Ax B Cx D As A Transformation Of Y Frac 1 X Mathematics Stack Exchange




The Graph Of Y Sqrt 4x X 2 Is Given Below Use Transformations To Create A Function Whose Graph Is As Shown Below Study Com
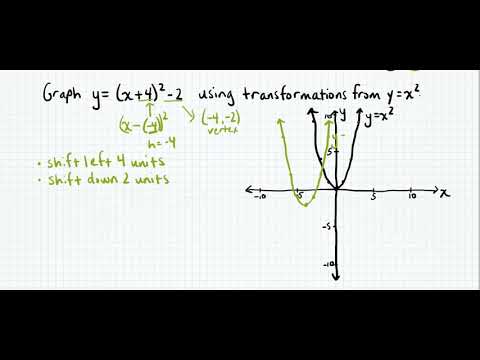



Graphing Transformations Of Y X 2 Youtube
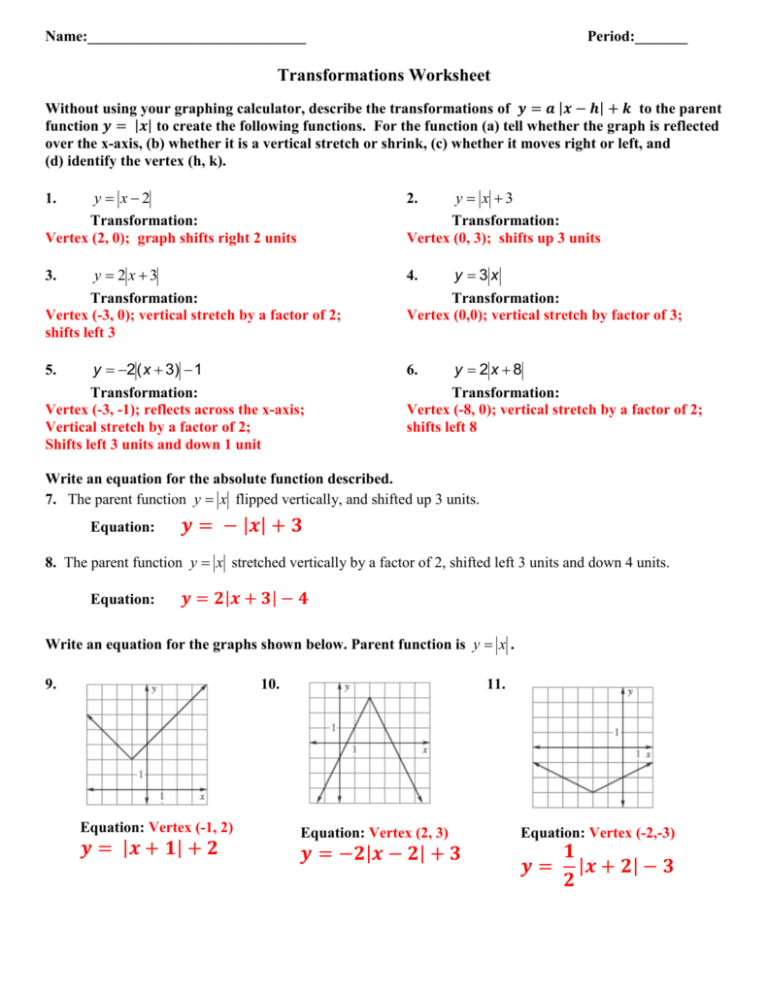



Absolute Value Transformations
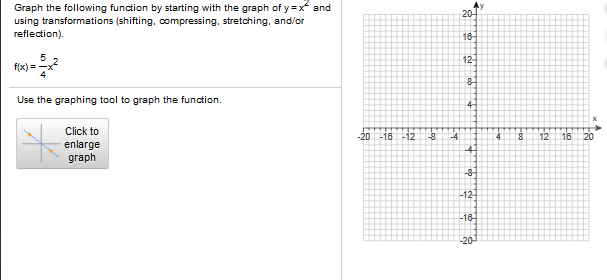



Solved Graph The Following Function By Starting With The Chegg Com



1 5 Shifting Reflecting And Stretching Graphs




Using Transformations To Graph Functions
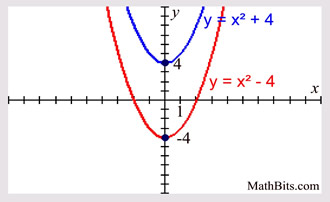



Parabola Parent Function Mathbitsnotebook Ccss Math



0 件のコメント:
コメントを投稿